扫雷游戏是微软推出的一款非常有意思的益智游戏，是Windows平台下一款非常经典的的小游戏，相信很多用户都玩过这款游戏吧？游戏目标是在最短的时间内根据点击格子出现的数字找出所有非雷格子，同时避免踩雷，游戏中有着多种难度可供挑战，欢迎大家下载体验。

很多人接触的第一款游戏可能就是windows操作系统自带的扫雷了，作为一款非常经典的益智类游戏，扫雷凭借简单的玩法深受好评，本次带来的是最经典的扫雷，也是人气最高的一个版本，造型更加酷炫，同时加入了爆炸音效，玩法简单却十分考验逻辑能力。

【扫雷基本介绍】

1、低中高3个难度等级。

2、可自定义面积和雷数。

3、觉得是雷的可以用小旗子给标出来，就不怕不小心点到了。

4、标了小旗子又感觉不是雷的，可以再点下变成问号模式，再点击下，问号又可消失。

【扫雷操作方法】

左键单击：在判断出不是雷的方块上按下左键，可以打开该方块。如果方块上出现数字，则该数字表示其周围3×3区域中的地雷数（一般为8个格子，对于边块为5个格子，对于角块为3个格子。所以扫雷中最大的数字为8）；如果方块上为空（相当于0），则可以递归地打开与空相邻的方块；如果不幸触雷，则游戏结束。

右键单击：在判断为地雷的方块上按下右键，可以标记地雷（显示为小红旗）。重复一次或两次操作可取消标记（如果在游戏菜单中勾选了“标记（？）”，则需要两次操作来取消标雷）。

双击：同时按下左键和右键完成双击。当双击位置周围已标记雷数等于该位置数字时操作有效，相当于对该数字周围未打开的方块均进行一次左键单击操作。地雷未标记完全时使用双击无效。若数字周围有标错的地雷，则游戏结束，标错的地雷上会显示一个“？”

【扫雷游戏攻略】

扫雷怎么玩？

开局的时候使用鼠标左键随机点击一个方格，方格即被打开并显示出方格中的数字；方格中数字则表示其周围的8个方格隐藏了几颗雷。鼠标右键是标记雷，同时按下左键和右键完成双击。当双击位置周围已标记雷数等于该位置数字时操作有效，相当于对该数字周围未打开的方块均进行一次左键单击操作。地雷未标记完全时使用双击无效。若数字周围有标错的地雷，则游戏结束，标错的地雷上会显示一个“×”。

扫雷的核心思想：九宫格。

圈内“1”表示它周围的八个格子只有一个地雷，那我么就把剩余那一个没显示的格子右键标记为雷（红旗）。

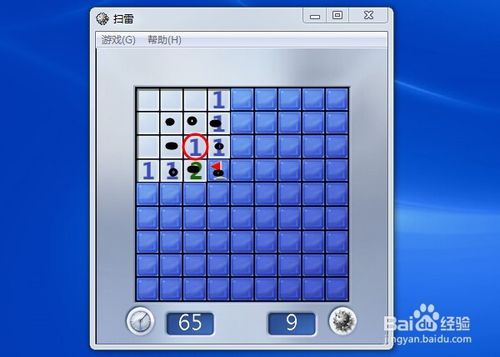
然后发现，红旗上方也有个“1”，而它所表示的雷已被标出，那么，我们左右键同时按这个数字，就会把它右边的三个格子同时打开。

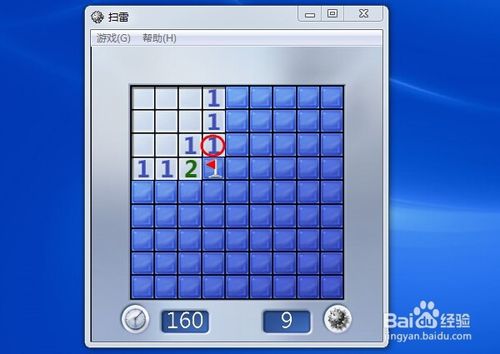
这里，换个想法，当我们标出一个雷后，可以，以这个雷为中心，找它周围的八个格子的数字，去一一对应。

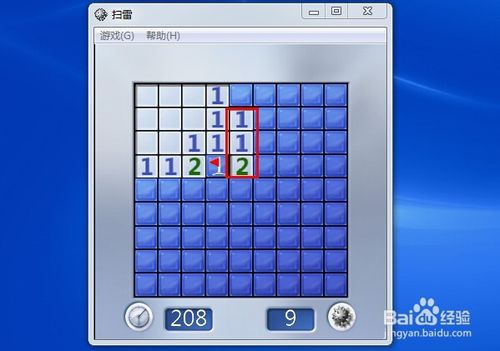
如图所示。我们发现，红旗的右上角又有一个“1”，继续重复操作，左右键同时按这个数字。

就出现了这个图示，继续重复操作。玩个几盘就会非常熟悉了。

1、如果无法判定某方块是否有雷，请用右键单击两次给它标记一个问号 (?)。以后，您可以用鼠标右键单击方块一次将该方块标记为地雷或者或用鼠标右键单击方块两次去掉标记。

2、如果某个数字方块周围的地雷全都标记完，可以指向该方块并同时点击鼠标左右键，将其周围剩下的方块挖开。如果编号方块周围地雷没有全部标记，在同时使用两个按钮单击时，其他隐藏或未标记的方块将被按下一次(即闪烁一下)。

3、寻找常见的数字组合，这通常会指示地雷的常见组合。例如，在一组未挖开的方块的边上相邻的三个数字 2-3-2 表示这三个数旁边有一排有三个地雷。

【扫雷游戏技巧】

扫雷如何判断雷

1、边角的1对应的角肯定是雷，这也是扫雷中最常见的情形。

2、边上的两个2并排对应的两个块肯定是雷

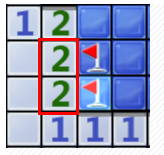
3、边角的3对应的3个块肯定是雷

4、孤立的3对应的3个块肯定是雷

5、孤立的4对应的4个块肯定是雷

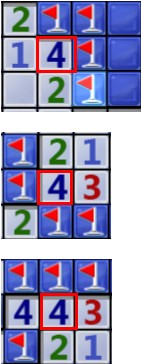
6、孤立的5对应的5个肯定是雷

7、两个1夹一个2的1，两个1下面对应的块肯定是雷

8、孤立的2对应的两个块肯定是雷

9、已知3的左边两个是雷，那么3的下边两个中肯定有一个是雷，所以第二个1下边的那个块肯定不是雷。

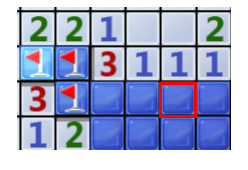
10、已知2的左边一个是雷，所以2的下边两个中肯定有一个是雷，所以1的右边3个块都不是雷。

11、上边那个1对应的两个角块中有一个是雷，所以下边那个1下边的3个块都不是雷。

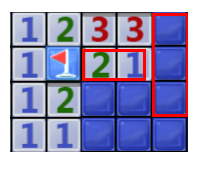
12、两个并排的3对应的3个块都是雷。

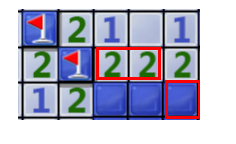
13、两个并排的2，已知左边那个2的左边是雷，则右边那个2的右下角那个肯定也是雷。

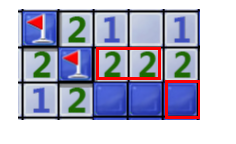
14、已知右边两个竖着的1的左边两个块中有个个是雷，则左边那两个1下方的两个块都不是雷。

15、1和2孤立地排在一起，则2要从下方3个块中选两个，肯定不会是左边两个，所以2的右下角那个肯定是雷，而1和2下边两个块中有1个是雷，所以1左下角那个肯定不会是雷。

16、一个3和一个2并排在一起，已知3上边那个是雷，则3左下角那个块肯定是雷，而2右下角那个块肯定不是雷。

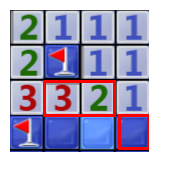
17、两个2并排在一起，且已知右边那个2正上方那个块是雷，则它的左边两个中肯定只有一个是雷，并且左边那个2的左边3个块都不是雷。

【扫雷基本公式】

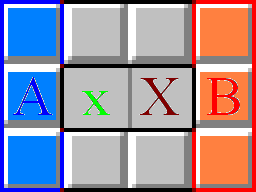
如上图:大Ｘ与小ｘ分别代表两个已知的相临数字，周围方块数量设定如下：

Ａ区域方块数为Ａ，Ｂ区域方块数为Ｂ，Ａ区域雷数为ａ，Ｂ区域雷数为ｂ，公共区域雷数为ｎ

当Ｘ＝ｘ+Ｂ时，Ｂ区域方块全是雷，Ａ区域方块全是数。

论证过程：

原假设：ｘ＞ｎ　┓

┣　Ｘ＞ｎ＋Ｂ　┓

Ｘ＝ｘ＋Ｂ　　　┛　　　　　　　┣　ｎ＋ｂ＞ｎ＋Ｂ　→　ｂ＞Ｂ

Ｘ＝ｎ＋ｂ　┛

显然ｂ＜＝Ｂ　∴原假设不成立　→　ｘ＝ｎ　┓

┣　ａ＝０

ｘ＝ｎ＋ａ　┛

ｘ＝ｎ　　　┓

Ｘ＝ｘ＋Ｂ　┣　ｎ＋Ｂ＝ｎ＋ｂ　→　Ｂ＝ｂ

Ｘ＝ｎ＋ｂ　┛

论题得证（以上证明过程不标雷，已经标的雷也当作方块处理）